Trig Ratios in Right Triangles
Basics on the topic Trig Ratios in Right Triangles
To calculate unknown side lengths and non-right angles of right triangles, trigonometric ratios are the keys to your success.
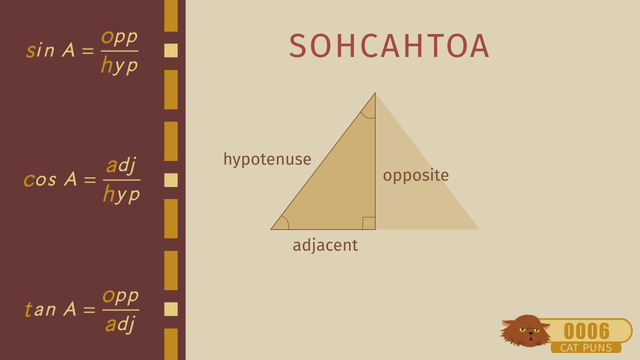
Just to refresh your memory, right triangles have a 90 degree angle. Look for the box in the corner to indicate a right angle. The side opposite the right angle is the hypotenuse, and the other sides are adjacent or opposite, depending on which angle you are considering.
The trig ratios you will use the most are sine, cosine, and tangent. Sine is the ratio of opposite to hypotenuse, cosine is the ratio of adjacent to hypotenuse, and tangent is the ratio of sine to cosine. Which ratio do you use to solve for an unknown measurement? That depends on what information is given in a problem. To help you solve problems, you’ll want to use a calculator that has the trig ratios or use a chart of the ratios.
Why do you study trig ratios? The ratios are very useful to solve real world problems. Before you hike up a steep mountain trail, do you want to know the distance of the trail? If you know the height of the mountain and one of the non-right angles, with the trig ratios you can calculate the measurement. Maybe you forgot to bring your calculator along on the hike – still it’s awesome to know that you can figure this out. To learn more, watch this video.
Define trigonometric ratios and solve problems involving right triangles
CCSS.MATH.CONTENT.HSG.SRT.C.6
Transcript Trig Ratios in Right Triangles
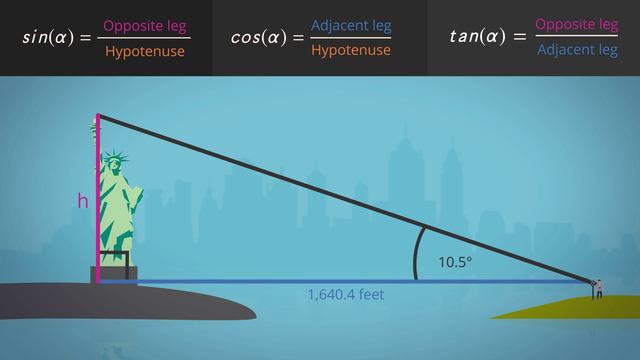
While visiting NYC, Kevin gets a look at the Statue of Liberty. He wonders, how tall is this lady?
How to calculate the Height of the Statue of Liberty
He looks through the viewing binoculars and notices the angle formed with the bottom of the base to the top of the statue's torch is ten and one-half degrees. How can Kevin use the trigonometry ratios of sine, cosine, and tangent of right triangles to calculate the unknown height of the Statue of Liberty?
Let's check out this situation. Can you see it builds a right triangle? Draw a line for the distance, then draw a line from the platform to the top of the triangle. From the viewfinder, we know the angle is ten point five degrees; write that in. Last draw in the line for the height. Don't forget to indicate the right angle.
Parts of a Right Triangle
Let's take a moment to review what we know about right triangles. The side opposite the right angle is named the hypotenuse, and the two sides adjacent to the right angle are the legs of the triangle. Across from angle alpha is the opposite side, and the adjacent side is between angle alpha and the right angle.
How to calculate sine, cosine, and tangent
To calculate the sine of angle alpha, sin(α), divide the length of the opposite leg by the length of the hypotenuse, and to find the cosine of angle alpha, cos(α), you divide the length of the adjacent leg by the length of the hypotenuse. For the tangent of angle alpha, tan(α), just divide the length of the opposite leg by the length of the adjacent leg.
Which Trigonometric Ratio should be used?
Which trigonometric ratio should you use to solve this problem? Sine, cosine, or tangent? Since you know the length of the adjacent leg, but not the hypotenuse, the tangent ratio is the best choice to calculate the length of the leg that is opposite angle alpha, the height of the Statue of Liberty.
Using the tangent ratio, set up the equation then just plug in the values you know. The tangent of 10.5 degrees times 1640.4 feet = the length of the opposite side.You will need to use your calculator to determine the tangent of 10.5 degrees, then multiply that number by 1640.4 feet to solve for the unknown height, the opposite leg.
She's a big one, 304 feet tall! Keven thinks trigonometric ratios are really fun and useful. The bird, on the other hand...
Trig Ratios in Right Triangles exercise
-
Find the trigonometric ratio that describes the angle of the given right triangle.
-
Evaluate the height of the Statue of Liberty using trigonometric ratios.
-
Solve for the height of each tree.
-
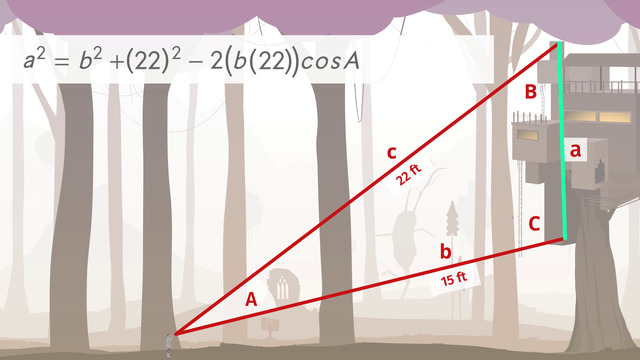
Determine the distance to the Eiffel Tower.
-
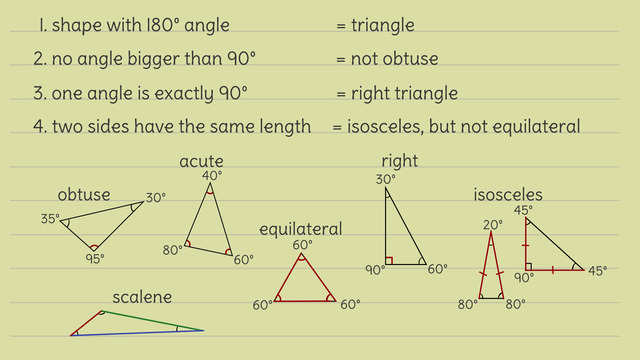
Identify the properties of right triangles.
-
Calculate the side lengths and angles of the right triangle.